🕑 Reading time: 1 minute
Lateral Load Distribution of Frame Building
In a two-dimensional moment-resisting frame, each joint typically has a maximum of three degrees of freedom: displacement in horizontal and vertical directions, and rotation. The total number of degrees of freedom is calculated as 3Nj, where Nj represents the number of joints in the frame. In practical applications, beams generally carry minimal axial force and experience negligible axial deformation. Consequently, the horizontal displacement at all beam-level joints remains consistent. Similarly, in most mid-rise buildings, the axial deformation of columns is insignificant, reducing the degrees of freedom to one rotation and one horizontal displacement per joint.
Considering the minimal rotational inertia associated with the rotational degree of freedom, it becomes feasible to further reduce the number of degrees through static condensation to one per storey for dynamic analysis purposes. In three-dimensional frames, each joint can potentially have up to six degrees of freedom, but ultimately there are typically three degrees of freedom per floor. Free vibration analysis of the building can be conducted by solving the (3N*3N) Eigenvalue problem, where N represents the number of storeys in the building. Once the natural frequency and mode shape are determined, the maximum seismic force at each storey level due to a given earthquake ground motion can be calculated.
Lateral Load Analysis of Moment Resisting Frame
Upon determining the design lateral loads for two-dimensional frames, analysis of the frame for member forces becomes crucial. This analysis can be carried out either through accurate computer analysis or via an approximate method, depending on project requirements. The approximate analysis is often performed during the preliminary design stage or to validate the results of computer-based analysis.
Two commonly employed methods for lateral load analysis are:
A. Portal frame method:
Portal frames serve as vital stiffness elements in building design, frequently employed at bridge entrances and as primary load-bearing components. These frames transfer horizontal forces applied at their tops to the foundation, resisting various forces such as wind, earthquake, and unbalanced traffic loading on bridge decks. Portal frames may be pin-supported, fixed-supported, or partially fixed. Let’s delve into the analysis of each case for a simple three-member portal frame.
In a typical pin-supported portal frame, statically indeterminate to the first degree, an assumption must be made to reduce it to a determinate structure. The elastic deflection diagram reveals a point of inflection approximately at the midpoint of the girder. Assuming a hinge exists at this point allows for the determination of reactions at the supports using statics. This results in equal horizontal reactions at the base of each column and other reactions as indicated. Moment diagrams for this frame are provided accordingly.
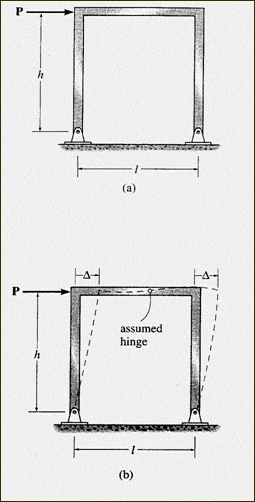
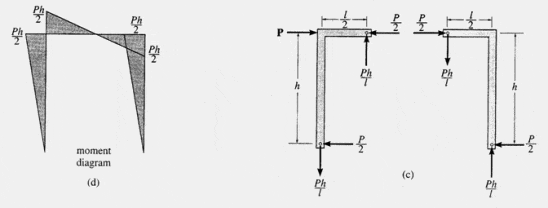
Fig. 1 Portal frame pin-supported at base
Fixed-Supported Portals: Portal frames with two fixed supports are statically indeterminate to the third degree. Assuming inflection points occur at the midpoints of all three members allows for the determination of reactions and moment diagrams for each member through dismemberment of the frame at the hinges. Equal horizontal reactions and moment diagrams for this frame are depicted accordingly.
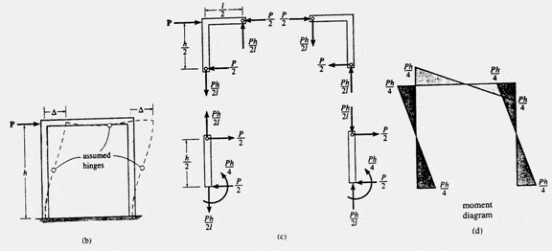
Fig. 2 Analysis of portal frames – Fixed at base
Partially Fixed (at the Bottom) Portal: Partially fixed portal frames assume slight rotations at the supports due to construction constraints. Engineers often place hinges at arbitrary points, such as h/3, to define inflection locations, along with hinges at the girder’s center. This assumption facilitates realistic estimates and conservative designs.
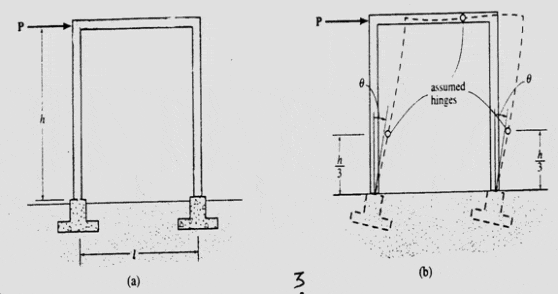
Fig. 3 Portal frame partially fixed at base
Trussed Frames: Trusses are employed in portal frames spanning large distances, maintaining column alignment under lateral loads. Analyzing trussed portals follows similar assumptions to simple portal frames, considering pin-supported or fixed-supported columns and inflection points.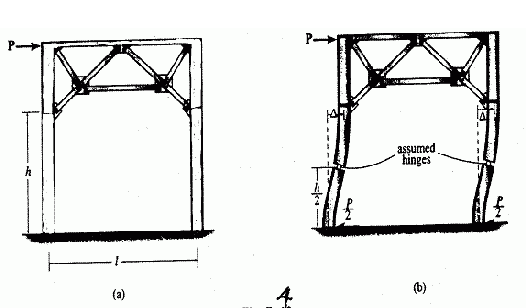
Fig. 4 Trussed frame fixed at base
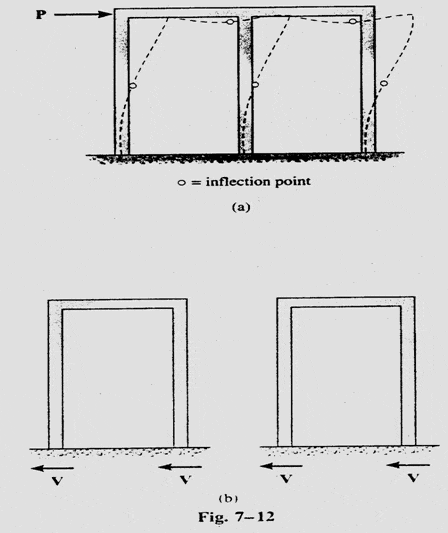
B. Cantilever method:
The cantilever method, akin to the action of a long cantilevered beam subjected to transverse loads, involves making assumptions to render the frame statically determinate. These assumptions include defining inflection points in columns and beams, and approximating axial forces based on column geometry and location. This method proves suitable for tall, slender frames or those with varied column cross-sections.
Overall, lateral load analysis of moment-resisting frames demands meticulous consideration of structural behavior under various loading conditions, ensuring structural integrity and safety.